SymPy-demo 4: Egenværdiproblemet

SymPy-demo 4: Egenværdiproblemet#

Demo af Christian Mikkelstrup og Hans Henrik Hermansen, Karl Johan Måstrup Kristiansen og Magnus Troen. Revideret 11-11-24 af shsp.

from sympy import *
init_printing()

I denne SymPy demo vil vi gerne vise, hvordan man bearbejder en matrix med det formål at løse egenværdiproblemet (dvs. at finde egenværdier, egenvektorer samt andre tilhørende egenskaber).

Vi vil arbejde på afbildningsmatricen

\[\begin{split} _e[\boldsymbol f]_e = \begin{bmatrix}6&3&12\\4&-5&4\\-4&-1&-10\end{bmatrix} \end{split}\]

for den lineære afbildning \(\boldsymbol f:\mathbb{R}^3\to \mathbb{R}^3\) med hensyn til standardbasen. Se kursuslærebogen for alle detaljerne i definitioner, terminologi, notation og sætninger, som vi benytter frit i det følgende.

eFe = Matrix([[6,3,12],[4,-5,4],[-4,-1,-10]])
eFe

\[\begin{split}\displaystyle \left[\begin{matrix}6 & 3 & 12\\4 & -5 & 4\\-4 & -1 & -10\end{matrix}\right]\end{split}\]

Egenværdier#

Vi opstiller den karakteristiske matrix \(\mathbf K(\lambda)= ~_e[\boldsymbol f]_e-\lambda\cdot \mathbf I_3\) som følger:

lamb = symbols('\lambda')
K = eFe - lamb * eye(3)
K

\[\begin{split}\displaystyle \left[\begin{matrix}6 - \lambda & 3 & 12\\4 & - \lambda - 5 & 4\\-4 & -1 & - \lambda - 10\end{matrix}\right]\end{split}\]

Det karakteristiske polynomium er determinanten, \(p(\lambda)=\mathrm{det}(\mathbf K(\lambda))\):

karakpol = K.det()
karakpol

../_images/df11c7722c7fcf30f8aedfaead2d2df49eb62592d18ad9606fd5ebecb4e93719.png

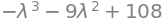
En SymPy-kommando kan gøre dette i ét trin, men bemærk, at fortegnet her er omvendt. Dette er dog ikke noget problem, da vi er interesserede i polynomiets rødder.

eFe.charpoly()

../_images/135e98286c7a3f690997c6a23c50eb1e8b636eb905d8c7f46a142fa6c1d4d8d0.png

Karakterligningen er det karakteristiske polynomium sat lig nul, \(\mathrm{det}(\mathbf K(\lambda))=0\):

karaklign = Eq(karakpol, 0)
karaklign

../_images/43e0d225dcd18a93978c819d8daba0a1a2516ea71d4f5fcf8be4c7c2accd2d24.png

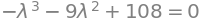
Den oprindelige afbildningsmatrix’ egenværdier kan nu findes enten ved at løse karakterligningen eller ved at benytte SymPys kommando .roots() til at bestemme rødderne i det karakteristiske polynomium:

roots(karakpol)

../_images/5d4aa86105537d932580e1af917a7cdf1fd9af24eff8ea01d61945f9021f1f1b.png

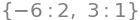
solveset(karaklign, lamb)

../_images/22baf7ec0a9179861225331ecf82aa91940a9dfc56e50a89558c2a49c951d7ac.png

Bemærk, at solveset() ikke fanger, at \(-6\) har algebraisk multiplicitet \(2\)! Hvis vi ikke vil risikere at misse denne multiplicitet, kan vi bede SymPy om en faktorisering som vist herunder, men ofte er roots() at foretrække i sådanne tilfælde.

factor(karakpol)

../_images/7d18dd1ea9e162104ec924b5c25f5b7af0f16654823f5fd87bbc499fa9c02fca.png

Egenvektorer#

For at finde egenvektorene tilhørende egenværdien \(-6\) skal vi finde samtlige løsninger til \(\mathbf K(-6)\,\mathbf x=\mathbf{0}\). Vi kan finde \(\mathbf K(-6)\) som følger:

K.subs(lamb, -6)

\[\begin{split}\displaystyle \left[\begin{matrix}12 & 3 & 12\\4 & 1 & 4\\-4 & -1 & -4\end{matrix}\right]\end{split}\]

Vi løser ved at bruge ovenstående koefficientmatrix med en højreside af nuller:

K.subs(lamb, -6).gauss_jordan_solve(zeros(3,1))

\[\begin{split}\displaystyle \left( \left[\begin{matrix}- \frac{\tau_{0}}{4} - \tau_{1}\\\tau_{0}\\\tau_{1}\end{matrix}\right], \ \left[\begin{matrix}\tau_{0}\\\tau_{1}\end{matrix}\right]\right)\end{split}\]

Vi aflæser af outputtet to lineært uafhængige egenvektorer tilhørende vores afbildning. Disse udspænder egenrummet for egenværdien \(-6\). Dette egenrum kan derfor opskrives om:

\[\begin{split} E_{-6}=\text{span}\left(\begin{bmatrix}-\frac{1}{4} \\ 1\\ 0 \end{bmatrix}, \begin{bmatrix} -1\\ 0\\ 1\end{bmatrix}\right). \end{split}\]

Vi tæller den geometriske multiplicitet til at være \(2\) (dimensionen af egenrummet) for egenværdien \(-6\).

Egenvektorerne hørende til egenværdien \(3\) findes på tilsvarende vis ved løsning af \(\mathbf K(3)\,\mathbf x=\mathbf{0}\), som læseren muligvis genkender som det samme som at finde kernen, \(\ker \mathbf K(3).\)

K.subs(lamb, 3).nullspace()

\[\begin{split}\displaystyle \left[ \left[\begin{matrix}-3\\-1\\1\end{matrix}\right]\right]\end{split}\]

Heraf ser vi, at \(E_3=\text{span}((-3,-1,1))\), samt at den geometriske multiplicitet er lig med den algebraiske multiplicitet på \(1\).

Indbyggede kommandoer til at finde egenværdier og egenvektorer#

Rent faktisk er der ikke behov for semi-manuelt at arbejde med karakteristiske matricer, karakteristiske polynomier og karakterligninger som ovenfor. SymPy kommer nemlig med indbyggede kommandoer, der kan anvendes direkte på afbildningsmatricen. Typisk vil den eneste grund til at udføre ovenstående semi-manuelle metoder være, hvis du har behov for omhyggeligt at gennemgå trinnene eller har brug for et mellemresultat. Er det ikke nødvendigt, så kan egenværdiproblemet meget hurtigt løses med følgende:

eFe.eigenvals()

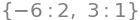
eFe.eigenvects()

\[\begin{split}\displaystyle \left[ \left( -6, \ 2, \ \left[ \left[\begin{matrix}- \frac{1}{4}\\1\\0\end{matrix}\right], \ \left[\begin{matrix}-1\\0\\1\end{matrix}\right]\right]\right), \ \left( 3, \ 1, \ \left[ \left[\begin{matrix}-3\\-1\\1\end{matrix}\right]\right]\right)\right]\end{split}\]

Kommandoen .eigenvects() giver endda alle data på én gang - både egenværdierne, deres algebraiske multiplicitet og tilhørende (lineært uafhængige) egenvektorer! Outputformatet, du ser ovenfor, er følgende:

\[\left[\Bigl(\lambda_1, \quad \operatorname {am}(\lambda_1),\quad \verb|egenvektorer for |\lambda_1\Bigr), \Bigl(\lambda_2, \quad \operatorname {am}(\lambda_2),\quad \verb|egenvektorer for |\lambda_2\Bigr),\ \ldots\right].\]

Hver parentes i outputtet indeholder oplysninger relateret til hver unik egenværdi.

Du tænker måske, at der stadig mangler lidt information: hvad med den geometriske multiplicitet for hver egenværdi? Men faktisk er denne værdi også tydelig i outputtet, da den blot er antallet af (lineært uafhængige) egenvektorer, der er knyttet til en egenværdi. Altså skal du blot tælle de egenvektorer, der vises for hver egenværdi. Egenrummene kan derefter skrives som udspændingen af de viste egenvektorer for hver egenværdi.

Du kan automatisere processen med at udtrække disse data fra outputtet fx med en for-løkke:

eigen_info = eFe.eigenvects()

for lmb, am_lmb, list_of_v in eigen_info:
    print(f'For egenværdien {lmb} med algebraisk multiplicitet {am_lmb} udspændes egenrummet af egenvektorerne')
    display(list_of_v)
    print(f'og den geometriske multiplicitet er {len(list_of_v)}' + '\n\n')

For egenværdien -6 med algebraisk multiplicitet 2 udspændes egenrummet af egenvektorerne

\[\begin{split}\displaystyle \left[ \left[\begin{matrix}- \frac{1}{4}\\1\\0\end{matrix}\right], \ \left[\begin{matrix}-1\\0\\1\end{matrix}\right]\right]\end{split}\]

og den geometriske multiplicitet er 2

For egenværdien 3 med algebraisk multiplicitet 1 udspændes egenrummet af egenvektorerne