SymPy-demo 0: Velkommen til Sympy og Jupyter Notebook

Demo af Karl Johan Måstrup Kristensen og Magnus Troen. Revideret 24-10-24 af shsp.

Indtil nu har I arbejdet med det, vi kalder kommandolinje-Python. Nu vil vi introducere dig til et par nye værktøjer, der vil gøre det muligt for dig at bruge Python som et egentligt CAS-værktøj:

• SymPy

• Jupyter Notebook

SymPy er en Python-pakke, der muliggør brugen af matematiske symboler, ligningsløsning og mere. Jupyter Notebook er et værktøj til at skrive Python-kode og tekst i samme dokument til professionel præsentation.

SymPy vil være dit primære CAS-værktøj i 01001 Matematik 1a og 01002 Matematik 1b, og kurserne vil anvende Jupyter Notebook til at præsentere demoer, eksempler, opgaver og projektoplæg. Denne demo er en introduktion til SymPys grundlæggende funktionaliteter samt til brugen af Jupyter Notebook.

Jupyter Notebook

Installation

Du har sandsynligvis allerede fulgt DTU Python supportens installationsguide (https://pythonsupport.dtu.dk/index.html) i andre kurser på DTU, hvilket betyder, at du formentlig allerede har alle nødvendige værktøjer installeret. Hvis ikke, så følg installationsguiden nu. En Jupyter Notebook-fil har filtypenavnet .ipynb.

Bemærk, at vores SymPy-demoer er skrevet i Jupyter Notebook, og du kan downloade dem som .ipynb via download-ikonet øverst på siden (oppe i højre hjørne). Prøv at downloade denne side nu, og følg resten af demoen i din egen editor.

Markdown

For at bygge bro mellem matematisk output fra software og det tilhørende matematiske ræsonnement tillader Jupyter Notebook, at eksekverbar kode og formateret tekst sammenblandes i ét dokument. Tekstformatering kan gøres ved hjælp af markdown-syntaks, der giver mulighed for overskrifter, fed skrift, kursiv og mere – se en komplet oversigt i den officielle markdown-syntaks guide. Bemærk også, at latex skrevet med $...$ eller $$...$$ renderes i tekst, så et latex-udtryk som $c=\sqrt{a^2+b^2}$ vises som det smukke udtryk: \(c=\sqrt{a^2+b^2}\). Er du ny til Latex, har vi tilføjet en kort Latex-gennemgang sidst i denne demo (under “Tips og Tricks” nedenfor).

Vi vil ikke gå yderligere i dybden med markdown og Latex-syntaks i dette kursus, men vi opfordrer dig til at lære at benytte dem til at skabe professionelt udseende dokumenter i alle dine kurser.

Kode og tekst samt genvejstaster

Bemærk: De genvejstaster, vi præsenterer i disse demoer, fungerer i kodeeditoren Visual Studio Code (VS Code), men de fleste vil også fungere i mange andre editorer.

Et Jupyter Notebook-dokument er opbygget af celler, der enten benævnes python og indeholder kode, eller markdown og indeholder tekst. Eksekvér (kør) en celle med genvejstaserne Ctrl+Enter, eller kør og spring til næste celle ved at taste Shift+Enter (hvis der ikke er nogen næste celle, vil Jupyter Notebook oprette en). Afprøv dette ved at skrive og køre følgende kode i en ny python-celle i en Jupyter Notebook-fil:

print("Søreme så, de har jo ret")

Søreme så, de har jo ret

Bemærk, at ikke kun python-celler, men også markdown-celler skal “eksekveres” – markdown renderes ikke, hvis du blot lader cellen stå i redigeringstilstand uden at køre den. Bemærk, at Shift+Enter lader dig bevæge dig ned gennem både python-celler og markdown-celler. Den lille blå markør til venstre for cellerne (i VS Code, men tilsvarende i andre editorer) indikerer, hvilken celle der aktuelt er valgt.

Tast Esc for at forlade redigeringstilstand i en celle uden at eksekvere den. Tast Enter eller dobbeltklik for at genåbne redigeringstilstand i en celle. Hvis du har downloadet denne demo, så prøv at åbne denne celle og redigere noget tekst. Når du ikke er i redigeringstilstand, kan du trykke m for at konvertere en Python-celle til en markdown-celle, og y for at konvertere en markdown-celle til en Python-celle.

Du tænker måske: “Skal jeg virkelig altid bruge print() for at få vist mine resultater?” Nej, Jupyter Notebook viser automatisk værdien af den sidste linje i en python-celle.

2+3+4+5+6*900

5414

Skriv flere værdier på linjen adskilt af komma, og de vises som et tupel (et liste-lignende objekt, som du måske er stødt på i dit tidligere arbejde med Python).

2+3+4+5+6*900, 4**2, 5-6

(5414, 16, -1)

Benyt Shift+Enter til at eksekvere Python-celler og se effekten af den skrevne kode i resten af denne og fremtidige demoer, hvis du downloader demoen og ser den i din editor (såsom VS Code). Hvis du læser denne demo på hjemmesiden, er output’ene fra python-celler vist som standard.

Se flere genvejstaster og tastekombinationer under “Tips og Tricks” sidst i denne demo.

Import sympy og dtumathtools

Fra dine programmeringskurser på DTU samt fra temaøvelserne har du sandsynligvis set pakker blive importeret på følgende måde:

import cmath
import numpy as np

Når en pakke er indlæst, kan de kommandoer, objekter og andet indhold, som pakken indeholder, tilgås. Med ovenstående metode til pakkeimport skal man skrive pakkens navn (eller det valgte præfiks) hver gang, man skal bruge en kommando eller et objekt fra pakken, for eksempel: cmath.polar() eller np.array().

For at gøre din kodning lettere og undgå behovet for præfikser kan pakken i stedet importeres på følgende måde; en importmetode som vi vil benytte gennem Matematik 1-kurserne:

from sympy import *
init_printing()

Linjen from sympy import ... giver adgang til SymPy-pakkens funktionaliteter uden præfiks. Du kan specificere det indhold, du har brug for fra pakken, ved at skrive f.eks. from sympy import sqrt, eller du kan indlæse alt pakkens indhold med asterisken *, som vi har gjort her.

Kommandoen init_printing() tvinger SymPy til at udskrive matematisk output fra Python-celler ved hjælp af flot LaTeX:

pi**3 + 3 * pi**2 + pi

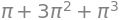
dtumathtools er en pakke lavet specifikt til Matematik 1-kurserne af DTU. Denne pakke vil gøre livet meget lettere, når det kommer til plotting. Du importerer dtumathtools på samme måde som sympy-pakken.

from dtumathtools import *

Symbolske og numeriske variable

Python uden SymPy lagrer sine outputs numerisk. Dette betyder, at alle tal og variable skal lagres i hukommelsen som et endeligt antal \(0\)’er og \(1\)’er. Studiet af numerisk matematik og lagring i digital elektronik og computervidenskab overlades til andre kurser ved DTU, men du bør være klar over, at dette kan føre til uventede og umiddelbart “forkerte” resultater i Python.

Eksempelvis er vi naturligvis alle enige om, at

\[ 0.3-(0.2+0.1) = 0. \]

Men Python er ikke enig:

0.3-(0.2+0.1)

Pythons output er ikke nøjagtig \(0\). Som konsekvens heraf vil fx en logisk sammenligning i Python med den logiske operator == give:

0 == 0.3-(0.2+0.1)

False

Vi skal altså passe på ved numeriske sammenligninger og generelt ved håndtering af decimaltal, de såkaldte floating point numbers.

Mange af sådanne problemer kan undgås ved at lade SymPy tage sig af matematikken. Udtrykkes tallene fra før som brøker, kan vi med SymPy håndtere dem mere passende med en dertilegnet SymPy-kommando så som S(tal) eller Rational(tæller, nævner) eller S('brøk'). SymPy vil nu holde tallene på rationel form (eksakt form fremfor approksimeret, numerisk form).

Rational(3,10)-(S(2)/10 + S('1/10'))

Kunne du tænke dig at vide mere om, hvordan S-kommandoen håndterer tallet bag kulisserne, så søg efter singletons i SymPy-dokumentationen.

Matematiske symboler og basale operatorer

Python tillader generelt ikke symbolsk matematik. Det tillader dig at definere værdier som symboler men ikke at definere udtryk, der indeholder variable eller ubekendte, som symboler. At skrive noget i stil med y=2*x+3 i Python vil give en fejl, da x er udefineret.

Symboler

Her ser vi styrken ved SymPy! Med SymPy kan vi definere vores variabel som et symbol på følgende måde, hvorefter vi kan benytte symbolet frit:

# Matematisk symbol
x = symbols('x')

y=2*x+3
y

Kommandoen symbols() er fundamentet under vores brug af Python som et CAS-værktøj.

Når man løser ligninger, reducerer udtryk osv., skal alle involverede symboler defineres, hvilket kan gøres på én gang:

x,y,z,l,p,t = symbols('x y z lambda phi theta')
x,y,z,l,p,t

Grundlæggende regnearter

De velkendte operatorer for de fire regnearter \(+,-,*,/\) vil opføre sig som I kender dem:

x+y, x-y, x*y, x/y

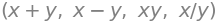
Andre matematiske operationer kan udføres med passende kommandoer fra SymPy, såsom kvadratrødder \(\sqrt{x}\) med sqrt(x) og den naturlige eksponentialfunktion \(\mathrm e^x\) med exp(x). Bemærk, at Python af og til kræver anderledes notation end hvad, vi er vant til. Dette gælder for potenser \(x^y\), som du opnår i Python ved at skrive x**y, og ikke ved at skrive x^y, som man ellers ville forvente i mange andre software.

x**y, sqrt(x), exp(x)

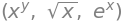
Eulers konstant er desuden defineret som E, hvis man foretrækker at skrive eksponentialfunktionen således:

E**x

Symboler med afgrænsninger (constraints)

Dit liv med SymPy vil blive meget lettere, hvis du definerer dine symboler med så meget information som muligt. Som standard vil SymPy antage, at der ikke er nogen begrænsninger på dine definerede symboler, hvilket betyder, at symbolerne antages at være komplekse. Så hvis du ved, at dine symboler f.eks. repræsenterer reelle tal, eller måske, at dit symbol ikke kan være \(0\), så kan det angives som følger:

# a er en reel variabel
a = symbols('a', real = True)

# b kan ikke være 0
b = symbols('b', nonzero = True)

# c er en reel variabel, der ikke kan være 0
c = symbols('c', real = True, nonzero = True)

Dette kan i nogle tilfælde reducere den tid, SymPy skal bruge i eksekveringen af senere operationer, og i andre tilfælde vil det være afgørende for overhovedet at få et svar. Derudover lader det SymPy reducere udtryk mere, end hvad der måske ellers var muligt, som følgende eksempel viser.

Eksempel på symboler med og uden afgrænsninger

Dette eksempel definerer udtrykket: \(\displaystyle\frac{\sqrt{x_1^2 + x_2^2}}{\sqrt{|x_1^2 + x_2^2|}},\quad x_1,x_2 \in \mathbb{R}.\)

Lad os først forestille os, at vi “glemmer” at angive de givne afgrænsninger. Vi skriver blot:

# Matematiske symboler uden constraints
x1,x2 = symbols('x1,x2')

udtryk_x = sqrt(x1**2 + x2**2)/sqrt(abs(x1**2 + x2**2))
udtryk_x

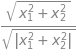
Her giver SymPy det fulde input som output uden nogen reduktion overhovedet.

Men prøv selv at justere dette i nedenstående Python-celle ved at tilføje argumentet real = True, som vi så ovenfor.

# Symboler med afgrænsninger (constraints)
x1,x2 = symbols('x1,x2') # <- Ændr denne linje for at afgrænse x1 og x2 til de reelle tal 

udtryk_y = sqrt(x1**2 + x2**2)/sqrt(abs(x1**2 + x2**2))
udtryk_y

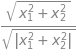
Resultatet bør blive, at SymPy nu er i stand til at reducere udtrykket betydeligt. Så det vil ofte være en fordel af give SymPy alle tilgængelige oplysninger om symboler.

Ligninger

Lighedstegnet = anvendes i Python til at definere værdier til variabler, og dobbelt lighedstegn == er en logisk operator, der straks evaluerer en sandhedsværdi. Hvordan kan vi så opskrive egentlige ligninger, når lighedstegn er reserveret til andre formål?

Definér ligninger

Det kan SymPy hjælpe dig med! Benyt blot kommandoen Eq(), hvori venstresiden og højresiden af ligningen adskildes af et komma. For eksempel kan ligningen \(x^2=\frac13 y\) skrives som Eq(x**2, S('1/3')*y). Husk først at definere alle involverede ukendte som symboler.

x,y = symbols('x,y')
lign = Eq(x**2, y*S('1/3'))
lign

Nu hvor dine outputs er hele ligninger og derfor mere komplicerede for Python at generere, kan det ske, at du pludselig ser output uden Latex-rendering. Hvis det sker, har du sandsynligvis glemt at tilføje eller køre init_printing() tidligere i dit dokument – men så du kan altid gå tilbage og køre det.

Løs ligninger

Vi gav en navn til ligningen ovenfor og kaldte den lign. Dermed kan vi hente ligningen, når den skal benyttes senere. Vi kan f.eks. prøve at løse ligningen ved brug af en solver-kommando i SymPy kaldet solveset(ligning, variabel):

losn = solveset(lign, x)
losn

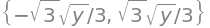
Outputtet fra solveset() vil altid være en matematisk mængde, som indeholder alle løsningerne. I dette eksempel har vi to løsninger. Skal nogle bestemte af løsningerne benyttes senere hen, kan de tilgås ved, at løsningsmængden først konverteres til en liste, hvorfra du derefter kan udtrække den ønskede løsning via indeksering:

liste_af_løsninger = list(losn)

liste_af_løsninger[0], liste_af_løsninger[1]

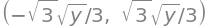
eller mængden kan gennemløbes ved brug af fx en for-løkke:

for losning in losn:
    display(losning)

Uendeligt mange løsninger: solveset() vs solve()

Det smarte ved disse sæt er dog, at hvis vi løser periodiske funktioner såsom

()\[\begin{equation} \sin(x) = 0 \end{equation}\]

Viser SymPy alle løsninger

lign = Eq(sin(x), 0)
solveset(lign, x)

Anvender vi i stedet SymPys ældre (og forældede) solve()-kommando, får vi kun nogle få af løsningerne:

solve(lign, x)

Af den grund vil vi primært benytte solveset() her i Matematik 1a og 1b.

Begrænsning af løsninger

Nogle gange ønskes kun løsninger inden for \(\mathbb{R}\). solveset() giver som standard alle løsninger i \(\mathbb{C}\), medmindre andet angives. Andet kan angives ved at tilføje et tredje argument til funktionen: solveset(ligning, variabel, definitionsmængde), som definerer den ønskede definitionsmængde, hvorfra løsninger skal findes.

Som et eksempel har ligningen

x = symbols('x')
lign = Eq(exp(x), 1)
lign

uendeligt mange løsninger, når \(x\in \mathbb{C}\),

solveset(lign, x)

men kun en enkelt løsning, når \(x\in\mathbb{R}\),

solveset(lign, x, S.Reals)

Ofte-benyttede afgrænsninger angivet med SymPy er bl.a. følgende:

• S.Reals

• S.Complexes

• Interval(0, 1)

Matematiske funktioner

Benyt en standard Python-funktion

Fra jeres Python-programmeringskurser ved DTU kender I allerede til følgende måde at definere Python-funktioner på:

# Standard Python-funktion
def f(x):
    return x**2

x = symbols('x')
f(x)

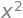
Ovenstående eksempel på en Python-funktion definerer den matematiske funktion \(f(x)=x^2\), og du kan nu udregne funktionsværdier ved at skrive f(2) og f(10) og tilsvarende. Denne type Python-funktion kan godt håndtere SymPy-objekter, men den kan give problemer ved dybere matematisk arbejde såsom differentiering.

Benyt substitution

Som et alternativ kan vi derfor definere matematiske funktioner ved blot at tildele udtrykkene til variabler:

# Matematisk funktion
fx = x**2

x = symbols('x')
fx

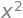
Dog kan vi nu ikke skrive fx(2) for at finde funktionsværdier, men det klarer vi blot med .subs(variabel,værdi), der erstatter \(x\) med en værdi:

# Substituterer x = 2
fx.subs(x, 2)

Dictionaries

.subs() kan også håndtere dictionaries, hvis vi vil indsætte flere værdier. Dictionaries er en datatype i python med formen

{x: 1, y: 2}

eller

dict(x = 1, y = 2).

Lad os som et eksempel se på følgende udtryk, hvori vi indsætter værdier for to variable:

# Funktion af to variable
fxy = x*y

x,y = symbols('x,y')

# Indsætter x=1, y=2
fxy.subs({x: 1, y: 2}), fxy.subs(dict(x = 1, y = 2))

Matematiske funktioner defineret på denne måde kan differentieres med diff(funktion, variabel, orden). I første kodelinje herunder differentieres der fx i det første udtryk med hensyn til \(x\) og i det næste udtryk med hensyn til \(x\) to gange (den andenordens afledte), mens der i den anden kodelinje udføres partiel differentiering af en funktion af to variable, i første udtryk med hensyn til \(y\) og i næste udtryk med hensyn til \(x\):

diff(fx, x, 1), diff(fx, x, 2)

diff(fxy, y,1), diff(fxy,x,1)

Komplekse tal

I SymPy er den imaginære enhed \(i\) defineret som I.

I

Komplekse tal kan altså skrives som:

# Ved at bruge S(1)/2, eller alternativt S('1/2'), vises 1/2 som en brøk fremfor som 0.5
z = S(1)/2 + I * sqrt(3)/2
z

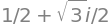
Vi har et stort arsenal af værktøjer til rådighed i SymPy til arbejdet med et komplekst tal \(z\)’s komponenter. For eksempel kan vi bede SymPy adskille reeldelen og imaginærdelen ved brug af .as_real_imag():

z.as_real_imag()

Eller vi kan finde modulus og argument af et kompleks tal med arg() og arg():

abs(z), arg(z)

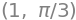
Den komplekst konjugerede findes også nemt med conjugate().

conjugate(z)

Simplificeringer og tvungne reduceringer

SymPy viser ikke altid den mest reducerede form af et udtryk. Hvor meget outputtet er reduceret, afhænger af kompleksiteten af udtrykket samt af, hvad der kom før. Overvej for eksempel dette lille udtryk:

z/(5*z)

I tilfælde som dette kan kommandoen simplify() benyttes til at tvinge outputtet ned på sin simplest mulige (mest reducerede) form:

simplify(z/(5*z))

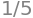
simplify() virker generelt og ikke kun på komplekse udtryk. Så, løber du ind i problemer med udtryk, der ikke vil reducere ordentligt i Python, så er det et forsøg værd at prøve simplify(). Hjælper det ikke, kan du definere variablerne med deres afgrænsninger (constraints), som vi så tidligere i demoen, og hvis heller ikke det virker, kan du være nødsaget til at reducere udtrykket i hånden.

Skift imellem komplekse former

Du vil ofte få behov for at skulle konvertere et komplekst tal til sin polære (eksponentielle) form eller til sin rektangulære form. Sidstnævnte opnås med .rewrite(sin) eller .rewrite(cos).

# z konverteres til polær form (manuelt)
z_exp = abs(z) * exp(arg(z) * I)
z_exp

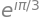
# z konverteres til rektangulær form
z_rekt = z_exp.rewrite(cos)
z_rekt

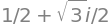
I nogle tilfælde kan .rewrite(exp) benyttes til at konvertere til polær (eksponentiel) form som i følgende eksempel:

# Ny rektangular form
t = symbols('t')
z1_rekt = cos(pi/3 * t) + I*sin(pi/3 * t)
z1_rekt

z1_rekt.rewrite(exp)

Hvis denne kommando ikke virker, er der ikke andet for end at konvertere til polær form manuelt.

Plots og dtumathtools, et kort indblik

Som nævnt tidligere er Python-pakken dtumathools udviklet specifikt for at gøre jeres Matematik 1-oplevelse på DTU nemmere. I denne pakke finder du kommandoer, som du ellers kun ville finde tilsvarende udgaver af i specialiserede matematiske software så som Maple (programmet der blev benyttet i tidligere udgaver af kurset). dtumathtools er hovedsageligt brugbar til nemt at lave flotte plots.

Vi vil gå mere i dybden med, hvordan man laver tilpassede og avancerede plots, når det bliver relevant. For nu vil vi blot vise nole simplere plots, som du kan bruge til at sikre dig, at pakken er korrekt installeret og virker som den skal.

Plots

Har du endnu ikke importeret pakken, så gør det nu.

from dtumathtools import *

Lad os definere nogle symboler til brug i nedenstående eksempler.

# symboler defineres
x,y = symbols('x,y,')

Plot funktion af én variabel

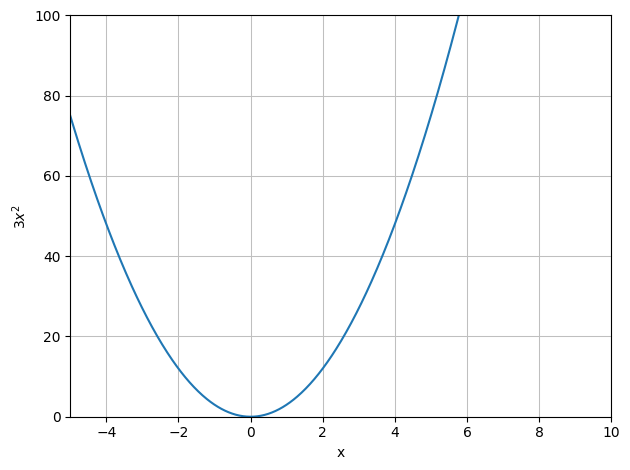
dtuplot.plot plotter funktioner af én variabel. Bemærk at du kan angive et væld af parametre for at tilpasse dit plot:

funk = 3*x**2
dtuplot.plot(funk, xlim = [-5,10], ylim = [0,100], xlabel = 'x', ylabel = '$3x^2$' )

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f795b4ef2e0>

Plot ligninger

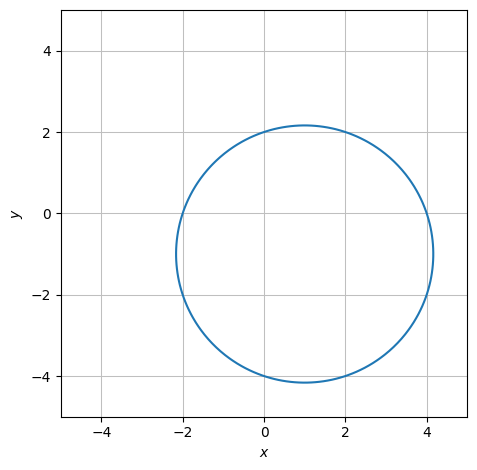
dtuplot.plot_implicit plotter ligninger og uligheder:

lign = Eq((x - 1)**2 + (y+1)**2, 10)
dtuplot.plot_implicit(lign, (x,-5, 5), (y,-5, 5), aspect="equal")

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f795b5716d0>

Plot parameterfremstillinger (parametriseringer)

dtuplot.plot_parametric plotter parameterfremstillinger i to dimensioner.

# Parameterfremstilling
vektor_funk = Matrix([x*cos(x), sin(x)])
dtuplot.plot_parametric(*vektor_funk, (x,0,2*pi))

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f795b2267f0>

Hold øje med de kommende demoer i de kommende uger for mere vedr. plots. dtumathtools-pakken er hjemmelavet af DTU og har derfor ikke nogen offentlig, officiel dokumentation - men vi kommer til at gå dybere ind i anvendelsen af pakken, efterhånden som plots bliver mere relevante, særligt i Matematik 1b.

Tips og tricks

SymPy-dokumentation

Det materiale, vi har valgt at vise i denne demo, er kun et lille udsnit af, hvad SymPy har af funktionalitet. Vi anbefaler dig at gøre dig bekendt med SymPy-dokumentationen, da den vil kunne besvare spørgsmål, som vi ikke havde tænkt på, da vi skrev disse demoer. Dokumentationen vil udvide din viden om og dine færdigheder i brugen af SymPy betydeligt.

Dokumentationen kan findes her:

• https://docs.sympy.org/latest/reference/index.html.

Bemærk, at du kan få info direkte fra Python om en bestemt kommando eller objekt ved blot at tilføje et spørgsmålstegn ? efter navnet på kommandoen eller objektet. Se nedenfor, men bemærk, at når du kører disse kodelinjer, vises der en større tekst med info fra dokumentationen:

Eq?

diff?

Brug af software til eksamenen i Matematik 1a

Til eksamenen i Matematik 1a i december er elektroniske hjælpemidler tilladt i den ene del. Vi anbefaler, at du træner med SymPy igennem semesteret, så du bliver ekspert i brugen af SymPy op til denne del af eksamenen. Men husk, at du ikke har adgang til internettet under eksamenen. For en sikkerheds skyld anbefaler vi derfor, at du downloader SymPy-dokumentationen lokalt til din computer fra følgende Github-link inden eksamen, så du nemt kan finde syntaks, kommandonavne, objekter osv., som du ellers bare ville have googlet.

• sympy/sympy

Vælg PDF eller HTML, når du downloader dokumentationen, da de andre links på Github-siden er til download af pakkens kildekode. Når du downloader som HTML, kan du se og bladre igennem de downloadede dokumenter på samme måde, som du kan på SymPy-dokumentationens website.

Markdown og matematiske udtryk med Latex

Hvis du er ny til Latex men gerne vil begynde at bruge det, så er dette afsnit en hurtig Latex-introduktion til dig.

Markdown-cellerne i Jupyter Notebook kan vise matematiske udtryk formateret med den såkaldte LaTeX-syntaks. Vi har benyttet Latex til at præsentere matematik i denne tekst, og det vil vi fortsætte med i alle fremtidige demoer. Latex kan tilføjes dit dokument på mange måder, men for at komme i gang vil vi her præsentere dig for to centrale metoder.

Inline Latex vs Latex på egen linje

Inline math-miljøer laves ved at skrive $udtryk$ direkte i tekst i en markdown-celle. Brug dette til at lave fyldige tekstlinjer, såsom: Lad $x\in\mathbb{R}$, og lad $P_2: \mathbb{R}\rightarrow\mathbb{R}$ betegne et vilkårligt andengradspolynomium., hvilket vil blive vist som følgende tekstlinje:

Lad \(x\in\mathbb{R}\), og lad \(P_2: \mathbb{R}\rightarrow\mathbb{R}\) betegne et vilkårligt andengradspolynomium.

Til større udtryk, der fortjener deres egen linje, benyttes $$udtryk$$. Dette vil centrere og vise udtrykket med mere plads end inline-udtryk. Skrives fx $$\lambda = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$$, fås følgende:

\[ \lambda = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \]

Bemærk her, hvordan brøker skrives med \frac{tæller}{nævner}. Du kan opløfte eller sænke ved at skrive $$x^2 \quad \text{og} \quad x_2$$:

\[x^2\quad \text{og}\quad x_2\]

Ekstra afstand og tekst inde i selve Latex-udtrykket blev i øvrigt også tilføjet her.

Dedikerede miljøer

Til større portioner af formateret matematik, såsom matricer eller ligningssystemer, findes der ofte et dedikeret LaTeX-miljø til formålet, som angives ved $\begin{miljø} ... \end{miljø}$. Følgende matrix kan som et eksempel skrives som $$\begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9 \end{bmatrix}$$:

\[\begin{split} \begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9 \end{bmatrix} \end{split}\]

Bemærk, hvordan \\ adskiller rækker, mens & adskiller kolonner. Disse tegn bruges også i det følgende miljø skrevet som $$\begin{aligned} -x_2+x_3&=2\\ 2x_1+4x_2-2x_3&=2\\ 3x_1+4x_2+x_3&=10\\ \end{aligned}$$, der opstiller et ligningssystem pænt, hvor & sikrer ensretning af linjerne:

\[\begin{split}\begin{aligned} -x_2+x_3&=2\\ 2x_1+4x_2-2x_3&=2\\ 3x_1+4x_2+x_3&=10\\ \end{aligned}\end{split}\]

Som du kan se, er LaTeX et helt andet sprog end Python/SymPy, og det anvender egne kommandoer, der omkranser deres input med krøllede parenteser. LaTeX er rig på funktionalitet og indeholder en enorm mængde kommandoer og indbyggede miljøer, og du kan bruge det til at vise stort set alt. Vi anbefaler, at du søger på internettet efter flere eksempler på LaTeX-syntaks, som du kan anvende i din daglige brug i projekter og rapporter. Der behøves ikke meget Latex-viden, før du kan skabe fyldige og professionelle matematiske afleveringsopgaver.

Konvertér SymPy-output til Latex

Det kan være irriterende at skulle skrive SymPy-outputs om til LaTeX-syntaks, særligt når der er tale om større outputs. Heldigvis har SymPy kommandoen print_latex(), der konverterer SymPy-outputs til LaTeX-kode:

a,b,c,lamda = symbols('a:c, lambda')
udtryk = Eq(lamda, (-b+sqrt(b**2-4*a*c))/(2*a))

print_latex(udtryk)

\lambda = \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}

Så kan du kopiere dette output og indsætte det direkte imellem Dollar-tegn, hvilket i dette eksempel vill give:

\[ \lambda = \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a} \]

Genvejstaster i VS Code

Du bør gøre dig selv bekendt med VS Codes indbyggede genvejstaster og tastekombinationer. Vi nævnte ganske få i starten af denne demo, og Microsoft har samlet mange flere til VS Code i disse cheatsheets:

• Windows og Linux

• macOS

Hvis du anvender en anden editor end VS Code, så har den helt sikkert nogle tilsvarende - hvis ikke de samme - genvejstaster, som du bør lære at kende.

Hvis ovenstående cheatsheets virker uoverskuelige, så husk blot denne tastekombination, afhænging af dit styresystem:

Windows eller Linux	macOS
Ctrl+Shift+P	CMD+Shift+P

Dette får en søgemenu til at poppe frem i VS Code. Heri kan du skrive nogenlunde, hvad du ønsker at gøre. Nogle nyttige søgetermer er:

• insert cell below eller insert cell above

• create notebook

• change cell to code eller change cell til markdown

Prøv det herunder. Klik på Python-cellen, få søgemenuen frem ved en passende tastekombination, og skift derefter cellen frem og tilbage imellem python-kode og markdown:

lign = Eq(x**2 - 2 * x + 1, 0)
lign

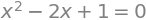
Når den ønskede handling dukker op, kan den vælges med piletasterne og med et tryk på Enter.

Hvis denne handling har en genvejstast, kan den ses i højre side, og hvis ikke, eller hvis man ikke er tilfreds med den eksisterende, kan man klikke på tandhjulet i højre side og lave sin egen genvejstastekombination.

Opret ny Jupyter Notebook

Åbn søgemenuen med:

Windows eller Linux	macOS
Ctrl+Shift+P	CMD+Shift+P

Søg på og vælg “Create: New Jupyter Notebook”. Dette opretter en blank Notebook.

Den nye Notebook gemmes og navgives med:

Windows eller Linux	macOS
Ctrl+S	CMD+S

Lav nye celler

Hold din musemarkør lige over eller under en celle. Så får du muligheden for at vælge mellem en celle til “Code” eller “Markdown”, som vil blive oprettet dér, hvor man er.

Er der endnu ikke oprettet nogen celler, er de to muligheder altid være synlige.

Alternativt kan man også benytte

Windows eller Linux	macOS
Ctrl+Shift+P	CMD+Shift+P

og søge på og vælge “Notebook: insert”. Her vil man kunne se alle muligheder for indsættelse af nye celler.

Eksekveringsrækkefølge

Fra arbejde med .py-filer (python script-filer) og command line-programmering er vi vandt til, at kode læses oppefra og ned. I Jupyter Notebook er dette ikke tilfældet.

Jo, indenfor den enkelte Python-celle eksekveres kode oppefra og ned, men forskellige celler eksekveres i den rækkefølge, du kører dem. Hvis en variabel defineres i en celle, så gælder den for hele Notebook’en, så snart cellen eksekveres, uanset hvor cellen er placeret; dvs. variablen gælder også for celler længere oppe i dokumentet.

Prøv for eksempel af eksekvere følgende fire Python-celler i den viste rækkefølge:

# Celle 1
a = 1

# Celle 2
a = 5

# Celle 3
a = 2

# Celle 4
a + 2

Og prøv så at eksekvere kun celle 2 og dernæst celle 4. Resultatet af udregningen i celle 4 afhænger tydeligvis af, hvilken definition af \(a\), der er sket senest. Definerer man en variabel flere gange, vil den gældende definition nemlig være den seneste, der er blevet kørt.

Hvis du pludselig oplever spøjse resultater, kan det derfor skyldes, at nogle variable allerede er defineret - dette sker nemt, når man arbejder dynamisk i sit dokument. Så af og til kan det være nødvendigt at eksekvere sine kommandoer fra starten af i rette rækkefølge - eller måske vil man ligefrem genstarte sin Python-kerne, eller blot redefinere sine symboler på ny med fx symbols(), fx før hver ny opgave i en aflevering for at rense eksisterende variabler.