Opgaver – Lille Dag

Opgaver – Lille Dag#

Opgave 1: Fra grader til radiantal og omvendt#

I denne opgave genopfriskes konverting fra grader til radiantal og omvendt.

Spørgsmål a#

Angiv de radiantal der svarer til vinkelmål \(30, 60, 120, 135\) og \(300\) grader.

Svar

\(\frac{\pi}{6}\), \(\frac{\pi}{3}\), \(\frac{2\pi}{3}\), \(\frac{3\pi}{4}\), \(\frac{5\pi}{3}\). Generelt: \(x\) grader svarer til radiantal \(x \pi / 180.\)

Spørgsmål b#

Tegn enhedscirklen i et \((x,y)\)-koordinatsystem med centrum i Origo. Afsæt punkter på enhedscirklen svarende til buelængderne

\[\pi\,,\, \frac{\pi}{3}\,, \,\frac{-\pi}{6}\,, \,-\frac{\pi}{6}\,, \,\frac{7\pi}{12}\,,\,-\frac{3\pi}{2}\,,\,\frac{7\pi}{4}\,.\]

Hvilke vinkelmål i grader svarer de til?

Svar

\(180\), \(60\), \(330\), \(330\), \(105\), \(90\), \(315\). Generelt: buelængden \(x\) svarer til \(180x/\pi\) grader hvis \(x \in [0,2\pi[\). Hvis \(x \not\in [0,2\pi[\), lægges først et multiplum af \(2\pi\) til således at udkomsten ligger i intervallet \([0,2\pi[\).

Opgave 2: Cosinus og sinus repetition#

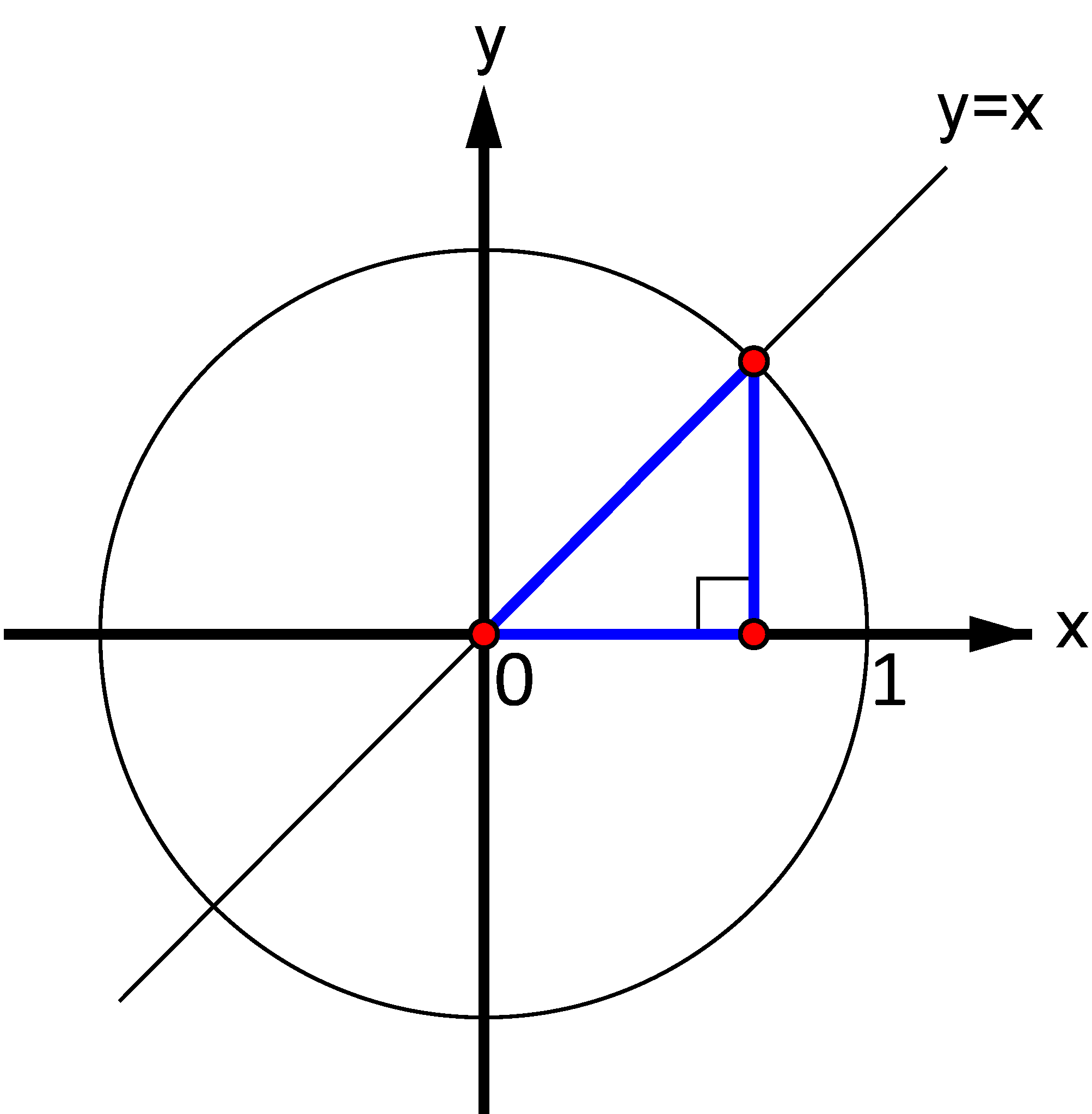
Spørgsmål a#

Benyt figuren (den blå trekant) til geometrisk bestemmelse af de eksakte værdier for \(\,\displaystyle{\cos\left(\frac{\pi}{4}\right)}\,\) og \(\,\displaystyle{\sin\left(\frac{\pi}{4}\right)}\,.\)

Hint

Husk at Pythagoras’ sætning medfører at \(\cos^2(x)+\sin^2(x)=1\) for all reelle tal \(x\).

Svar

De giver begge \(\frac{\sqrt{2}}{2}\,. \)

Spørgsmål b#

Bestem ved hjælp af symmetribetragtninger tallene

\[ \cos\left(p\,\frac{\pi}{4}\right)\,\,\,\mathrm{og}\,\,\,\sin\left(p\,\frac{\pi}{4}\right) \,\,\,\mathrm{for}\,\,\,p \in \{3, 5, 7, -1, -3, -5, -7\}\,. \]

Svar

\((-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}),(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}),(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}),(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}),(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}), (-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}),(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}).\)

Spørgsmål c#

Det oplyses at \(\,\displaystyle{\cos\left(\frac{\pi}{6}\right)}=\frac{\sqrt 3}{2}\,\) og \(\,\displaystyle{\sin\left(\frac{\pi}{6}\right)}=\frac{1}{2}\,.\) Indtegn punktet

\[\, \displaystyle{\left(\cos\left(\frac{\pi}{6}\right)\,,\,\sin\left(\frac{\pi}{6}\right)\right)} \,\]

på en enhedscirkel og find ved hjælp af symmetribetragtninger tallene

\[ \cos\left(p\,\frac{\pi}{6}\right)\,\,\,\mathrm{og}\,\,\,\sin\left(p\,\frac{\pi}{6}\right) \,\,\,\mathrm{for}\,\,\,p \in \{2, 4, 5, 7, 8, 10, 11\}\,. \]

Hint

Bemærkning: i Appendiks 1 fra lærebogen, som står straks efter det sidste kapitel, kan du finde en enhedscirkel, samt værdien af cosinus og sinus i visse “pæne” vinkler.

Opgave 3: Funktionerne \(\mathrm{arccos}\), \(\mathrm{arcsin}\) og \(\mathrm{arctan}\).#

I denne opgave betragtes de inverse trigonometriske funktioner \(\mathrm{arccos}\), \(\mathrm{arcsin}\) og \(\mathrm{arctan}\). Hvis du har behov for at genopfriske eller se graferne til disse funktioner, så kan du kigge på Afsnit 2.3 fra lærebogen (især underafsnittet “De inverse trigonometriske funktioner”).

Spørgsmål a#

Angiv tallene \(\,\displaystyle{\mathrm{arccos}\left(\frac{1}{2}\right),\,\mathrm{arcsin}\left(-\frac{\sqrt 3}{2}\right)}\) og \(\displaystyle{\mathrm{arctan}(-1)}\,.\)

Svar

\(\frac{1}{3} \, \pi\), \(-\frac{1}{3} \, \pi\), \(-\frac{1}{4} \, \pi\).

Spørgsmål b#

Lad \(x \in \mathbb{R}\) og \(y \in [-1,1]\) være reelle tal. Lad \(P\) være det logiske udsagn \(\mathrm{arccos(y)}=x\) og \(Q\) det logiske udsagn \(y=\cos(x)\). Vis at \(P \Rightarrow Q\) er sandt, men at \(Q \Rightarrow P\) ikke behøves at være sandt.

Hint

Til \(P \Rightarrow Q\): hvad sker der hvis man anvender \(\cos\)-funktionen på begge sider af lighedstegnet i \(P\)?

Til \(Q \Rightarrow P\): kan du finde \(x \in \mathbb{R}\) og \(y \in [-1,1]\) således at \(Q\) er sandt, men \(P\) ikke?

Opgave 4: Cosinus og sinus repetition, del 2.#

Denne opgave bygger videre på Opgave 3.

Spørgsmål a#

Der er givet mængderne \(\,A=\left[\,0\,,\,2\pi\,\right]\,\) og \(\,B=\left[\,-\pi\,,\,\pi\,\right]\,.\)

Løs ligningen \(\,\displaystyle{\cos(x)=\frac{1}{2}}\,\) inden for hver af mængderne \(\,A,\,B\,\) og \(\,\Bbb R\,.\)

Hint

En løsning til ligningen fås direkte fra spørgsmål 3a, fordi ifølge spørgsmål 3b \(\mathrm{arccos}(y)=x\) medfører at \(y=\cos(x).\) Find nu samtlige løsninger i \(\mathbb{R}\) ved at lave en skitse af grafen til \(\cos\)-funktionen.

Svar

Indenfor \(A\) er løsningerne: \(\,\frac{\pi}{3}\,\) og \(\,\frac{5\pi}{3}\,.\)

Indenfor \(B\) er løsningerne \(\,\frac{-\pi}{3}\,\) og \(\,\frac{\pi}{3}\,.\)

Indenfor \(\mathbb{R}\) er løsningerne \(\,\frac{-\pi}{3}+p\cdot 2\pi\,\) og \(\,\frac{\pi}{3}+p\cdot 2\pi\,\) hvor \(\,p \in \Bbb Z\,.\)

Spørgsmål b#

Løs ligningen \(\,\displaystyle{\sin(x)=-\frac{\sqrt 3}{2}}\,\) inden for hver af mængderne \(\,A,\,B\,\) og \(\,\Bbb R\,.\)

Svar

Indenfor \(A\) er løsningerne: \(\,\frac{4\pi}{3}\,\) og \(\,\frac{5\pi}{3}\,.\)

Indenfor \(B\) er løsningerne: \(\,\frac{-2\pi}{3}\,\) og \(\,-\frac{\pi}{3}\,.\)

Indenfor \(\mathbb R\) er løsningerne: \(\,\frac{4\pi}{3}+p\cdot 2\pi\,\) og \(\,\frac{5\pi}{3}+p\cdot 2\pi\,\) hvor \(\,p \in \Bbb Z\,.\)

Opgave 5: Polære koordinater#

Spørgsmål a#

Givet tallene \(z_1=1+i\sqrt{3}\,\), \(z_2=-1+i\sqrt{3}\,\), \(z_3=-1-i\sqrt{3}\,\) og \(z_4=1-i\sqrt{3}\,\).

  1. Indtegn \(z_1\), \(z_2\), \(z_3\) og \(z_4\) i den komplekse talplan og giv tallenes rektangulære koordinater.

  2. Find modulus (også kendt som absolutværdi) til \(z_1\), \(z_2\), \(z_3\) og \(z_4\). Konkluder at de fire tal ligger på en cirkel med centrum i \(0\). Hvad er cirklens radius?

  3. Bestem hovedargumenet for \(z_1\), \(z_2\), \(z_3\) og \(z_4\) og giv tallenes polære koordinater.

Hint

Angående bestemmelse af modulus og hovedargument: se Theorem 4.3.1 (og eventuelt Figur 4.5) fra lærebogen.

Hint

\(\mathrm{arctan}(\sqrt{3})=\pi/3\), fordi \(\tan(\pi/3)=\frac{\sin(\pi/3)}{\cos(\pi/3)}=\frac{\sqrt{3}/2}{1/2}=\sqrt{3}.\)

Svar

Delvist svar:

\(z_1\): Tallets rektangulære koordinater er \((1,\sqrt{3})\), mens dets polære koordinater er \((2,\pi/3)\).

\(z_2\): Tallets rektangulære koordinater er \((-1,\sqrt{3})\), mens dets polære koordinater er \((2,2\pi/3)\).

\(z_3\): Tallets rektangulære koordinater er \((-1,-\sqrt{3})\), mens dets polære koordinater er \((2,-2\pi/3)\).

\(z_4\): Tallets rektangulære koordinater er \((1,-\sqrt{3})\), mens dets polære koordinater er \((2,-\pi/3)\).

Spørgsmål b#

Nogen skal finde de polære koordinater for det komplekse tal \(\,-2+2i\,\,\). Vedkommende laver følgende: først beregnes

\[\sqrt{(-2)^2+2^2}\]

som giver \(\,2\sqrt{2}\,\) til absolutværdien. Efterfølgende beregnes

\[\mathrm{arctan}\left(\frac{2}{-2}\right)\]

som giver svaret \(\,\displaystyle{-\frac {\pi}4}\,.\)

En del af svaret er forkert, men hvor ligger fejlen?

Spørgsmål c#

Find absolutværdi og hovedargument for det følgende komplekse tal:

\[\displaystyle{-\frac{1}{6}+\frac{i}{2\sqrt{3}}}\,.\]

Svar

absolutværdi \(\frac{1}{3}\), hovedargument \(\frac{2}{3} \, \pi\)

Spørgsmål d#

Om tre komplekse tal \(z_1\), \(z_2\) og \(z_3\) oplyses angående deres modulus og argument at:

\[|z_1|=4 \quad \text{og} \quad \mathrm{arg}(z_1)=-\pi,\]
\[|z_2|=2 \quad \text{og} \quad \mathrm{arg}(z_2)=4\pi/3\]

og

\[|z_3|=6 \quad \text{og} \quad \mathrm{arg}(z_3)=21\pi/4.\]

Bemærk at tallenes hovedargument ikke er givet, men kun et muligt argument.

  1. Bestem tallenes hovedargument.

  2. Find tallenes rektangulære form.

Hint

Hovedargumentet af et komplekst tal skal ligge i intervallet \(]-\pi,\pi].\) For hvert givet argument, læg et smart valgt multiplum af \(2\pi\) til, således at resultatet ligger i \(]-\pi,\pi].\) Læs eventuelt begyndelsen af Section 4.3 fra lærebogen for mere information om argument og hovedargument af et komplekst tal.

Hint

Angående rektangulær form: Ligning (4.4) fra lærebogen kan bruges her.

Svar

  1. Hovedargumenterne er: \(\pi\), \(-2\pi/3\) og \(-3\pi/4\).

  2. Tallene på rektangulær form: \(-4\), \(-1-i \, \sqrt{3}\), \(-3 \, \sqrt{2} - i \, 3 \, \sqrt{2}\).

Contents